Empirical Bayesian kriging (EBK), geçerli bir kriging modeli oluşturmanın en zor yönlerini otomatikleştiren jeoistatistiksel bir enterpolasyon yöntemidir. Geostatistical Analyst’deki diğer kriging yöntemlerinde doğru sonuçları almak için parametreleri ayarlamanız gerekir, ancak EBK, bu parametreleri bir alt-set ve simülasyon işlemi aracılığıyla otomatik olarak hesaplar.

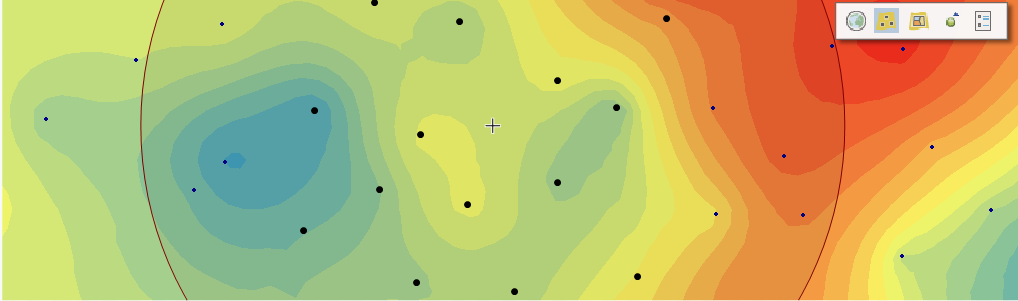
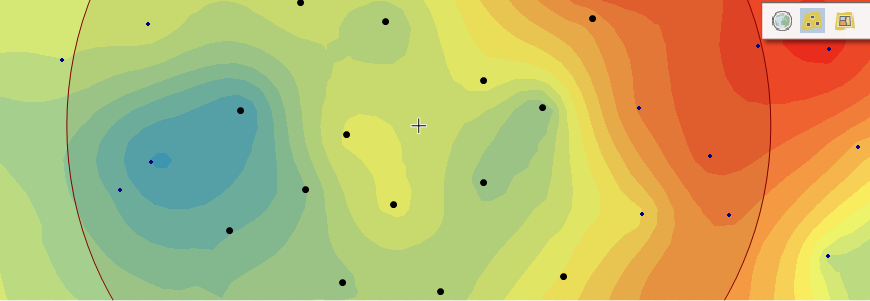
Empirical Bayesian Kriging’in diğer kriging yöntemlerinden farkı altta yatan semivariogramı tahmin etmesi ve ortaya çıkan hatayı hesaplamasıdır. Diğer kriging yöntemleri bilinen veri konumlarından semivariogramı hesaplar ve bilinmeyen yerlerde tahmin yapmak için bu tek semivariogramı kullanır; Bu süreç, tahmin edilen semivariogramın enterpolasyon bölgesi için doğru semivariogram olduğunu kısmen kabul eder. Semivariogram kestiriminin belirsizliğini dikkate almayan diğer kriging yöntemleri, standart tahmin hatalarını hafife alır.

Empirical Bayesian kriging aracı hem Geostatistical Wizard’da hem de  geoprocessing araçları içerisinde bulunmaktadır.

Avantaj ve Dezavantajlar

Avantajlar

• Minimum etkileşimli modelleme gerektirir.
• Standart tahmin hataları diğer kriging yöntemlerinden daha doğrudur.
• Orta derecede sabit olmayan verilerin doğru tahminlerini sağlar.
• Küçük veri kümelerinde diğer kriging yöntemlerinden daha doğrudur.

Dezavantajlar

• Nokta verileriniz, alt küme boyutu ve üst üste binme sayısı arttıkça işlem süresi etkilenecektir. Bir dönüşüm tipi seçerseniz(Empirical, Log empirical) ve  semivariogram model tipi için de K-Bessel veya K-Bessel Detrended seçilmişse, işlem süresi artacaktır. Bu parametreler  sonraki blog yazılarında açıklanacaktır.
• İşleme, özellikle raster’e çıktığında, diğer kriging yöntemlerinden daha yavaştır. Aracın sonucunun raster olarak alınması diğer kriging yöntemlerine göre daha yavaştır.
• Cokriging ve anisotropic düzeltmeler mevcut değildir.
• Log Empirical dönüşümü bir birinden uzak değerlere özellikle duyarlıdır. Bu dönüşümü, bir birinden uzak değerler içeren verilerle kullanırsanız, giriş noktalarınızın değerlerinden daha büyük veya daha küçük değerleri alabilirsiniz.

Semivariogram Tahmini

Diğer kriging yöntemlerinden farklı olarak , EBK’daki semivariogram parametreleri kısıtlı maksimum olasılık (REML) kullanılarak tahmin edilir. Büyük veri kümeleri için REML’nin hesaplama kısıtlamaları nedeniyle, giriş verileri ilk olarak belirli bir boyutta üst üste binen alt kümelere bölünür (varsayılan olarak her 100 nokta bir alt kümeye bölünür). Her alt kümede, semivariogramlar şu şekilde tahmin edilir:

1. Semivariogram alt kümedeki verilerden hesaplanır.
2. Bu semivariogramı model olarak alarak, alt kümedeki giriş konumlarının her birinde koşulsuz olarak yeni veriler simüle edilir.
3. Simüle edilmiş verilerden yeni bir semivariogram tahmin edilir.
4. 2. ve 3. adımlar belirtilen sayıda tekrarlanır. 1. adımda tahmin edilen semivariogram girdi verilerinin konumlarında yeni veri kümesini simüle etmek için kullanılır daha sonra simüle edilmiş veriler yeni semivariogramı tahmin etmek için kullanılır.

Bu süreç, her bir alt küme için çok sayıda semivariogram oluşturur ve bunlar birlikte çizildiğinde, sonuç, yoğunluk tarafından gölgelenen bir semivariogram dağılımıdır (daha koyu mavi renk, daha fazla semovariogram bu bölgeden geçer). Empirical semivariances mavi (+) ile temsil edilir. Ek olarak, dağılımın medyanı koyu kırmızı bir çizgi ile renklendirilmiş ve 25 ve 75’inci yüzdeler aşağıda gösterildiği gibi kırmızı kesikli çizgilerle renklendirilmiştir.

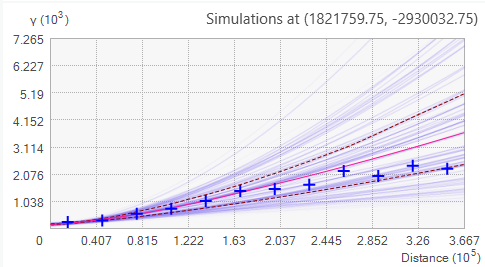
Simüle edilmiş semivariogramlar

Alt küme için simule edilen semivariogramların sayısı varsayılan olarak 100’e ayarlanır ve bu semivariogramların her biri, alt küme için gerçek semivariogramın bir tahminidir.

Her bir tahmin konumu için noktanın çevresindeki semivariogram spektrumlarından tekil semivariogram örneklerine dayalı bir örneklemeyle oluşturulan yeni bir semivariogram dağılımı kullanılarak hesaplanır. Örneğin, bir tahmin yerinin üç farklı alt kümede (arama komşuluğunda belirtildiği gibi) komşuları varsa, üç alt kümenin her birinden simüle edilmiş semivariogramlar kullanılarak hesaplanacaktır; Bu semivariogramlar olasılık değerlerine göre seçilmiştir.

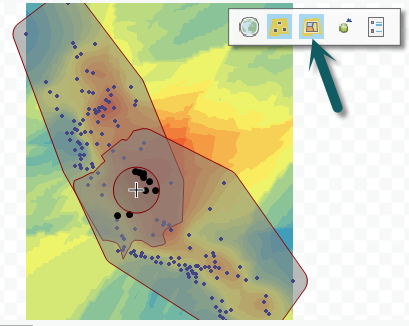
Geostatistical Wizard ile Empirical Bayesian Kriging’i çalıştırdığınızda tahmin edilen değeri hesaplamak için kullanılan alt kümeleri görebilirsiniz. Aşağıdaki görselde, tahmin yüzeyindeki imleç merkezdir. İmlecin etrafındaki küçük daire, arama merkezidir ve üst üste binen çokgenler, tahminleri hesaplamak için kullanılan iki alt kümede yer alan noktaları gösterir. Bu örnekte, haritanın ortasındaki noktalar her iki alt kümede de bulunur. Bu görselleştirmeyi mavi okla gösterilen buton ile açıp kapatabilirsiniz:

Kaynaklar

http://pro.arcgis.com/en/pro-app/help/analysis/geostatistical-analyst/what-is-empirical-bayesian-kriging-.htm